堆

堆(heap)是計(jì)算機(jī)科學(xué)中一類特殊的數(shù)據(jù)結(jié)構(gòu)的統(tǒng)稱，通常是一個(gè)可以被看做一棵樹的數(shù)組對(duì)象。

堆{k1,k2,ki,…,kn} (ki <= k2i,ki <= k2i+1)|(ki >= k2i,ki >= k2i+1), (i = 1,2,3,4...n/2)

關(guān)于堆：

堆中某個(gè)節(jié)點(diǎn)的值總是不大于或不小于其父節(jié)點(diǎn)的值； 堆總是一棵完全二叉樹（下面）。 將根節(jié)點(diǎn)最大的堆叫做最大堆或大根堆，根節(jié)點(diǎn)最小的堆叫做最小堆或小根堆。

完全二叉樹

說(shuō)到堆排序，就不能不提完全二叉樹，這些基本概念在網(wǎng)上到處都是，我摘了個(gè)最簡(jiǎn)單的。。

完全二叉樹：除最后一層外，每一層上的節(jié)點(diǎn)數(shù)均達(dá)到最大值；在最后一層上只缺少右邊的若干結(jié)點(diǎn)。

我自己總結(jié)認(rèn)為，正是因?yàn)橛邢旅鎯蓚€(gè)特點(diǎn)，

只允許最后一層有空缺結(jié)點(diǎn)且空缺在右邊，即葉子結(jié)點(diǎn)只能在層次最大的兩層上出現(xiàn)（存儲(chǔ)方式的規(guī)則性）； 若i>1，tree的雙親為tree[i div 2]（其父子結(jié)點(diǎn)值的規(guī)律性）；

才使得其進(jìn)行排序非常方便。

堆排序

堆排序求升序用大頂堆，求降序用小頂堆。

本例用求降序的小頂堆來(lái)解析。

堆排序步驟如下：

1、我們將數(shù)據(jù)（49、38、65、97、76、13、27、50）建立一個(gè)數(shù)組$arr；

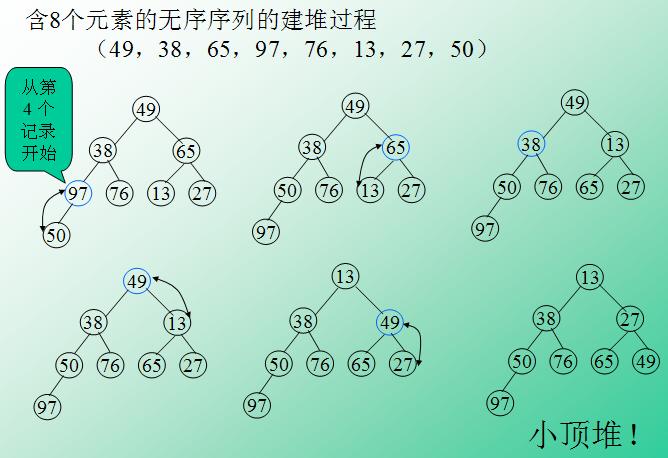
2、用數(shù)組$arr建立一個(gè)小頂堆（主要步驟，會(huì)在代碼注釋里解釋，下圖是用一個(gè)數(shù)組建立小頂堆的過(guò)程）；

3、將堆的根（最小的元素）與最后一個(gè)葉子交換，并將堆長(zhǎng)度減一，跳到第二步；

4、重復(fù)2-3步，直到堆中只有一個(gè)結(jié)點(diǎn)，排序完成。

堆排序的PHP實(shí)現(xiàn)

//因?yàn)槭菙?shù)組,下標(biāo)從0開始,所以,下標(biāo)為n根結(jié)點(diǎn)的左子結(jié)點(diǎn)為2n+1,右子結(jié)點(diǎn)為2n+2; //初始化值,建立初始堆$arr=array(49,38,65,97,76,13,27,50);$arrSize=count($arr);//將第一次排序抽出來(lái)，因?yàn)樽詈笠淮闻判虿恍枰俳粨Q值了。buildHeap($arr,$arrSize);for($i=$arrSize-1;$i>0;$i--){ swap($arr,$i,0); $arrSize--; buildHeap($arr,$arrSize); }//用數(shù)組建立最小堆function buildHeap(&$arr,$arrSize){ //計(jì)算出最開始的下標(biāo)$index,如圖,為數(shù)字'97'所在位置,比較每一個(gè)子樹的父結(jié)點(diǎn)和子結(jié)點(diǎn),將最小值存入父結(jié)點(diǎn)中 //從$index處對(duì)一個(gè)樹進(jìn)行循環(huán)比較,形成最小堆 for($index=intval($arrSize/2)-1; $index>=0; $index--){ //如果有左節(jié)點(diǎn),將其下標(biāo)存進(jìn)最小值$min if($index*2+1<$arrSize){ $min=$index*2+1; //如果有右子結(jié)點(diǎn),比較左右結(jié)點(diǎn)的大小,如果右子結(jié)點(diǎn)更小,將其結(jié)點(diǎn)的下標(biāo)記錄進(jìn)最小值$min if($index*2+2<$arrSize){if($arr[$index*2+2]<$arr[$min]){ $min=$index*2+2;} } //將子結(jié)點(diǎn)中較小的和父結(jié)點(diǎn)比較,若子結(jié)點(diǎn)較小,與父結(jié)點(diǎn)交換位置,同時(shí)更新較小 if($arr[$min]<$arr[$index]){swap($arr,$min,$index); } } }}//此函數(shù)用來(lái)交換下數(shù)組$arr中下標(biāo)為$one和$another的數(shù)據(jù)function swap(&$arr,$one,$another){ $tmp=$arr[$one]; $arr[$one]=$arr[$another]; $arr[$another]=$tmp;}

下面是排序的最終結(jié)果：

堆用來(lái)進(jìn)行全排序，時(shí)間復(fù)雜度是O(nlogn)

而快排用來(lái)全排序，平均時(shí)間復(fù)雜度也是O(nlogn)

但堆排序可以用來(lái)求 TopK 時(shí)，堆的時(shí)間復(fù)雜度為O(Klog2(n)，因?yàn)樗恍枰M(jìn)行 K 輪排序即可。

以上就是本文的全部?jī)?nèi)容，希望對(duì)大家的學(xué)習(xí)有所幫助，也希望大家多多支持好吧啦網(wǎng)。